Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 26, pp. 1-10.
Existence and uniqueness for a p-Laplacian
nonlinear eigenvalue problem
Giovanni Franzina, Pier Domenico Lamberti
Abstract:
We consider the Dirichlet eigenvalue problem
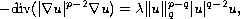
where the unknowns
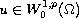 (the eigenfunction)
and
(the eigenfunction)
and
 (the eigenvalue),
(the eigenvalue),
 is an arbitrary
domain in
is an arbitrary
domain in
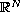 with finite measure,
with finite measure,
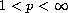 ,
,
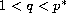 ,
,
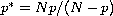 if
if
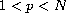 and
and
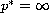 if
if
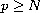 .
We study several existence and uniqueness results as well as
some properties of the solutions. Moreover, we indicate how to
extend to the general case some proofs known in the classical
case
.
We study several existence and uniqueness results as well as
some properties of the solutions. Moreover, we indicate how to
extend to the general case some proofs known in the classical
case
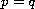 .
.
Submitted January 14, 2010. Published February 16, 2010.
Math Subject Classifications: 35P30.
Key Words: p-laplacian; eigenvalues; existence; uniqueness results
Show me the PDF file (262 KB),
TEX file for this article.
 |
Giovanni Franzina
Dipartimento di Matematica, University of Trento
Trento, Italy
email: g.franzina@email.unitn.it
|
|---|
 |
Pier Domenico Lamberti
Dipartimento di Matematica Pura e Applicata
University of Padova, Padova, Italy
email: lamberti@math.unipd.it
|
|---|
Return to the EJDE web page
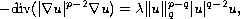
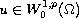 (the eigenfunction)
and
(the eigenfunction)
and
 (the eigenvalue),
(the eigenvalue),
 is an arbitrary
domain in
is an arbitrary
domain in
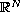 with finite measure,
with finite measure,
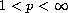 ,
,
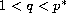 ,
,
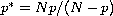 if
if
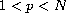 and
and
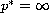 if
if
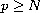 .
We study several existence and uniqueness results as well as
some properties of the solutions. Moreover, we indicate how to
extend to the general case some proofs known in the classical
case
.
We study several existence and uniqueness results as well as
some properties of the solutions. Moreover, we indicate how to
extend to the general case some proofs known in the classical
case
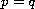 .
.

