Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 33, pp. 1-11.
Existence of multiple solutions for a p(x)-Laplace equation
Duchao Liu
Abstract:
This article shows the existence of at least three
nontrivial solutions to the quasilinear elliptic equation
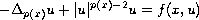
in a smooth bounded domain
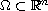 ,
with the nonlinear boundary condition
,
with the nonlinear boundary condition
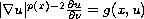 or the Dirichlet boundary condition
or the Dirichlet boundary condition
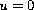 on
on
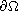 .
In addition, this paper proves that one solution is positive,
one is negative, and the last one is a sign-changing solution.
The method used here is based on Nehari results, on three
sub-manifolds of the space
.
In addition, this paper proves that one solution is positive,
one is negative, and the last one is a sign-changing solution.
The method used here is based on Nehari results, on three
sub-manifolds of the space
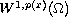 .
.
Submitted September 26, 2008. Published March 3, 2010.
Math Subject Classifications: 35B38, 35D05, 35J20.
Key Words: Critical points; p(x)-Laplacian; integral functionals;
generalized Lebesgue-Sobolev spaces.
Show me the PDF file (242 KB),
TEX file for this article.
 |
Duchao Liu
School of Mathematics and Statistics
Lanzhou University, Lanzhou 730000, China
email: liudch06@lzu.cn
|
|---|
Return to the EJDE web page
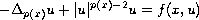
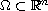 ,
with the nonlinear boundary condition
,
with the nonlinear boundary condition
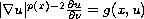 or the Dirichlet boundary condition
or the Dirichlet boundary condition
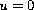 on
on
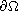 .
In addition, this paper proves that one solution is positive,
one is negative, and the last one is a sign-changing solution.
The method used here is based on Nehari results, on three
sub-manifolds of the space
.
In addition, this paper proves that one solution is positive,
one is negative, and the last one is a sign-changing solution.
The method used here is based on Nehari results, on three
sub-manifolds of the space
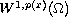 .
.
