Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 58, pp. 1-12.
A global curve of stable, positive
solutions for a p-Laplacian problem
Bryan P. Rynne
Abstract:
We consider the boundary-value problem
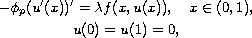
where
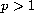 (
(
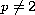 ),
),
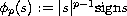 ,
,
 ,
,
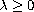 ,
and the function
,
and the function
![$f : [0,1] \times \mathbb{R} \to \mathbb{R}$](gifs/ag.gif) is
is
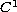 and
satisfies
and
satisfies
![$$\displaylines{
f(x,\xi) > 0, \quad (x,\xi) \in [0,1] \times \mathbb{R} ,\cr
(p-1)f(x,\xi) \ge f_\xi(x,\xi) \xi ,
\quad (x,\xi) \in [0,1] \times (0,\infty) .
}$$](gifs/ai.gif)
These assumptions on
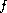 imply that the trivial solution
imply that the trivial solution
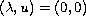 is the only solution
with
is the only solution
with
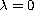 or
or
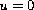 ,
and if
,
and if
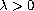 then any solution
then any solution
 is {\em positive},
that is,
is {\em positive},
that is,
 on
on
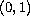 .
.
We prove that the set of nontrivial solutions
consists of a
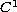 curve of positive solutions in
curve of positive solutions in
![$(0,\lambda_{max}) \times C^0[0,1]$](gifs/as.gif) ,
with a parametrisation of the form
,
with a parametrisation of the form
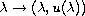 ,
where
,
where
 is a
is a
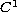 function defined on
function defined on
 ,
and
,
and
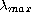 is a suitable weighted eigenvalue of the
is a suitable weighted eigenvalue of the
 -Laplacian
(
-Laplacian
(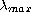 may be finite or
may be finite or
 ),
and
),
and
 satisfies
satisfies
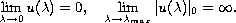
We also show that for each
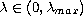 the solution
the solution
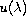 is globally asymptotically stable,
with respect to positive solutions
(in a suitable sense).
is globally asymptotically stable,
with respect to positive solutions
(in a suitable sense).
Submitted August 13, 2009. Published April 28, 2010.
Math Subject Classifications: 34B15.
Key Words: Ordinary differential equations; p-Laplacian;
nonlinear boundary value problems; positive solutions;
stability.
Show me the PDF file (286 KB),
TEX file for this article.
 |
Bryan P. Rynne
Department of Mathematics and the Maxwell Institute for
Mathematical Sciences
Heriot-Watt University
Edinburgh EH14 4AS, Scotland
email: bryan@ma.hw.ac.uk
|
|---|
Return to the EJDE web page
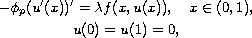
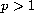 (
(
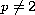 ),
),
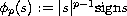 ,
,
 ,
,
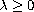 ,
and the function
,
and the function
![$f : [0,1] \times \mathbb{R} \to \mathbb{R}$](gifs/ag.gif) is
is
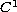 and
satisfies
and
satisfies
![$$\displaylines{
f(x,\xi) > 0, \quad (x,\xi) \in [0,1] \times \mathbb{R} ,\cr
(p-1)f(x,\xi) \ge f_\xi(x,\xi) \xi ,
\quad (x,\xi) \in [0,1] \times (0,\infty) .
}$$](gifs/ai.gif)
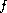 imply that the trivial solution
imply that the trivial solution
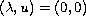 is the only solution
with
is the only solution
with
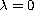 or
or
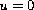 ,
and if
,
and if
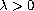 then any solution
then any solution
 is {\em positive},
that is,
is {\em positive},
that is,
 on
on
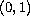 .
. 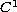 curve of positive solutions in
curve of positive solutions in
![$(0,\lambda_{max}) \times C^0[0,1]$](gifs/as.gif) ,
with a parametrisation of the form
,
with a parametrisation of the form
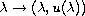 ,
where
,
where
 is a
is a
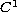 function defined on
function defined on
 ,
and
,
and
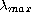 is a suitable weighted eigenvalue of the
is a suitable weighted eigenvalue of the
 -Laplacian
(
-Laplacian
(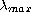 may be finite or
may be finite or
 ),
and
),
and
 satisfies
satisfies
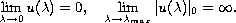
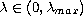 the solution
the solution
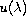 is globally asymptotically stable,
with respect to positive solutions
(in a suitable sense).
is globally asymptotically stable,
with respect to positive solutions
(in a suitable sense).
