Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 74, pp. 1-14.
A Holmgren type theorem for partial differential equations
whose coefficients are Gevrey functions
Masaki Kawagishi
Abstract:
In this article, we consider a uniqueness theorem of Holmgren type
for p-th order Kovalevskaja linear partial differential equations
whose coefficients are Gevrey functions. We prove that the
only
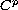 -solution to the zero initial-valued problem is
the identically zero function. To prove this result we use the
uniqueness theorem for higher-order ordinary differential
equations in Banach scales.
-solution to the zero initial-valued problem is
the identically zero function. To prove this result we use the
uniqueness theorem for higher-order ordinary differential
equations in Banach scales.
Submitted March 28, 2010. Published May 21, 2010.
Math Subject Classifications: 35A05, 35A10, 35G10.
Key Words: Banach scale; Gevery function; Holmgren type;
Uniqueness theorem.
Show me the PDF file (262 KB),
TEX file for this article.
 |
Masaki Kawagishi
Department of General Education College of Science
and Technology,
Nihon University
1-8-14 Kanda-Surugadai, Chiyoda-ku, Tokyo 101-8308, Japan
email: masaki@suruga.ge.cst.nihon-u.ac.jp
|
|---|
Return to the EJDE web page
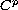 -solution to the zero initial-valued problem is
the identically zero function. To prove this result we use the
uniqueness theorem for higher-order ordinary differential
equations in Banach scales.
-solution to the zero initial-valued problem is
the identically zero function. To prove this result we use the
uniqueness theorem for higher-order ordinary differential
equations in Banach scales.
