Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 82, pp. 1-21.
Existence and uniqueness of classical solutions to
second-order quasilinear elliptic equations
Diane L. Denny
Abstract:
This article studies the existence of solutions to the
second-order quasilinear elliptic equation
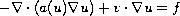
with the condition
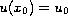 at a certain point
in the domain, which is the 2 or the 3 dimensional torus.
We prove that if the functions a, f, v satisfy
certain conditions, then there exists a unique classical solution.
Applications of our results include stationary heat/diffusion
problems with convection and with a source/sink, when
the value of the solution is known at a certain location.
at a certain point
in the domain, which is the 2 or the 3 dimensional torus.
We prove that if the functions a, f, v satisfy
certain conditions, then there exists a unique classical solution.
Applications of our results include stationary heat/diffusion
problems with convection and with a source/sink, when
the value of the solution is known at a certain location.
Submitted April 13, 2010. Published June 18, 2010.
Math Subject Classifications: 35A05.
Key Words: Existence; uniqueness; quasilinear; elliptic.
Show me the PDF file (311 KB),
TEX file for this article.
 |
Diane L. Denny
Department of Mathematics and Statistics
Texas A\&M University - Corpus Christi
Corpus Christi, TX 78412, USA
email: diane.denny@tamucc.edu
|
|---|
Return to the EJDE web page
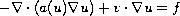
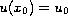 at a certain point
in the domain, which is the 2 or the 3 dimensional torus.
We prove that if the functions a, f, v satisfy
certain conditions, then there exists a unique classical solution.
Applications of our results include stationary heat/diffusion
problems with convection and with a source/sink, when
the value of the solution is known at a certain location.
at a certain point
in the domain, which is the 2 or the 3 dimensional torus.
We prove that if the functions a, f, v satisfy
certain conditions, then there exists a unique classical solution.
Applications of our results include stationary heat/diffusion
problems with convection and with a source/sink, when
the value of the solution is known at a certain location.
