Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 06, pp. 1-7.
A regularity criterion for the Navier-Stokes equations in terms
of the horizontal derivatives of the two velocity components
Wenying Chen, Sadek Gala
Abstract:
In this article, we consider the regularity for weak solutions
to the Navier-Stokes equations in
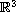 .
It is proved that if the horizontal derivatives of the two
velocity components
.
It is proved that if the horizontal derivatives of the two
velocity components
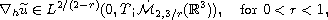
then the weak solution is actually strong, where
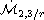 is the critical Morrey-Campanato
space and
is the critical Morrey-Campanato
space and
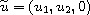 ,
,
 .
.
Submitted October 18, 2010. Published January 12, 2011.
Math Subject Classifications: 35Q30, 76F65.
Key Words: Navier-Stokes equations; Leray-Hopf weak solutions;
regularity criterion.
Show me the PDF file (218 KB),
TEX file for this article.
 |
Wenying Chen
College of Mathematics and Computer Science
Chongqing Three Gorges University
Wanzhou 404000, Chongqing, China
email: wenyingchenmath@gmail.com
|
|---|
| |
Sadek Gala
Department of Mathematics
University of Mostaganem
Box 227, Mostaganem 27000, Algeria
email: sadek.gala@gmail.com
|
|---|
Return to the EJDE web page
 .
It is proved that if the horizontal derivatives of the two
velocity components
.
It is proved that if the horizontal derivatives of the two
velocity components
 is the critical Morrey-Campanato
space and
is the critical Morrey-Campanato
space and
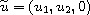 ,
,
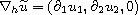 .
.
