Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 08, pp. 1-18.
Existence of global solutions to the 2-D subcritical dissipative
quasi-geostrophic equation and persistency of the initial regularity
May Ramzi, Ezzeddine Zahrouni
Abstract:
In this article, we prove that if the initial data
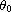 and
its Riesz transforms (
and
its Riesz transforms (
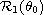 and
and
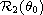 ) belong to the space
) belong to the space
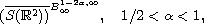
then the 2-D Quasi-Geostrophic
equation with dissipation
 has a unique global in time
solution
has a unique global in time
solution
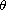 .
Moreover, we show that if in addition
.
Moreover, we show that if in addition
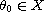 for some functional space
for some functional space
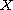 such as
Lebesgue, Sobolev and Besov's spaces then the solution
such as
Lebesgue, Sobolev and Besov's spaces then the solution
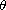 belongs to the space
belongs to the space
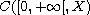 .
.
Submitted August 10, 2010. Published January 15, 2011.
Math Subject Classifications: 35Q35, 76D03
Key Words: Quasi-geostrophic equation; Besov Spaces
Show me the PDF file (343 KB),
TEX file for this article.
 |
May Ramzi
Département de Mathématiques
Faculté des Sciences de Bizerte, Tunisie
email: ramzi.may@fsb.rnu.tn
|
|---|
 |
Ezzeddine Zahrouni
Département de Mathématiques
Faculté des Sciences de Monastir, Tunisie
email: Ezzeddine.Zahrouni@fsm.rnu.tn
|
|---|
Return to the EJDE web page
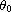 and
its Riesz transforms (
and
its Riesz transforms (
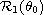 and
and
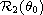 ) belong to the space
) belong to the space
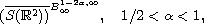
 has a unique global in time
solution
has a unique global in time
solution
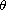 .
Moreover, we show that if in addition
.
Moreover, we show that if in addition
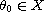 for some functional space
for some functional space
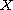 such as
Lebesgue, Sobolev and Besov's spaces then the solution
such as
Lebesgue, Sobolev and Besov's spaces then the solution
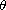 belongs to the space
belongs to the space
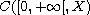 .
.

