If
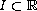 is an open interval and
is an open interval and
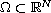 an open subset with
an open subset with
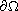 Lipschitz continuous, we show that the space
Lipschitz continuous, we show that the space
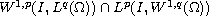 is continuously
embedded in
is continuously
embedded in
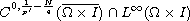 if
if
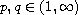 and
and
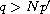 .
When
.
When
 ,
this coincides with Morrey's
embedding theorem for
,
this coincides with Morrey's
embedding theorem for
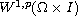 . While weaker
results have been obtained by various methods, including very
technical ones, the proof given here follows that of Morrey's
theorem in the scalar case and relies only on widely known
properties of the classical Sobolev spaces and of the Bochner
integral.
. While weaker
results have been obtained by various methods, including very
technical ones, the proof given here follows that of Morrey's
theorem in the scalar case and relies only on widely known
properties of the classical Sobolev spaces and of the Bochner
integral. This embedding is useful to formulate nonlinear evolution problems as functional equations, but it has other applications. As an example, we derive apparently new space-time Holder continuity properties for
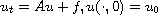 when
when
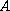 generates a
holomorphic semigroup on
generates a
holomorphic semigroup on
 .
.
