This article is a sequel to two earlier articles (one of them written jointly with R. Banuelos) on stability results for the Neumann eigenvalues and eigenfunctions of domains in
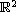 with
a snowflake type fractal boundary.
In particular we want our results to be applicable to the Koch snowflake
domain. In the two earlier papers we assumed that a domain
with
a snowflake type fractal boundary.
In particular we want our results to be applicable to the Koch snowflake
domain. In the two earlier papers we assumed that a domain
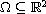 which has a snowflake type boundary
is approximated by a family of subdomains and that the Neumann heat
kernel of
which has a snowflake type boundary
is approximated by a family of subdomains and that the Neumann heat
kernel of
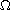 and those of its approximating subdomains satisfy a
uniform bound for all sufficiently small t>0. The purpose of this
paper is to extend the results in the two earlier papers to the
situations where the approximating domains are not necessarily
subdomains of
and those of its approximating subdomains satisfy a
uniform bound for all sufficiently small t>0. The purpose of this
paper is to extend the results in the two earlier papers to the
situations where the approximating domains are not necessarily
subdomains of
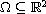 .
We then apply our results to the Koch snowflake
domain when it is approximated from outside by a decreasing sequence of
polygons.
.
We then apply our results to the Koch snowflake
domain when it is approximated from outside by a decreasing sequence of
polygons.
