Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 163, pp. 1-22.
Goursat problem for the Yang-Mills-Vlasov system
in temporal gauge
Marcel Dossa, Marcel Nanga
Abstract:
This article studies the characteristic Cauchy
problem for the Yang-Mills-Vlasov (YMV) system in temporal gauge,
where the initial data are specified on two intersecting
smooth characteristic hypersurfaces of Minkowski spacetime
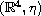 .
Under a
.
Under a
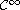 hypothesis on the data,
we solve the initial constraint problem and the evolution problem.
Local in time existence and uniqueness results are established
thanks to a suitable combination of the method of characteristics,
Leray's Theory of hyperbolic systems and techniques
developed by Choquet-Bruhat for ordinary spatial Cauchy
problems related to (YMV) systems.
hypothesis on the data,
we solve the initial constraint problem and the evolution problem.
Local in time existence and uniqueness results are established
thanks to a suitable combination of the method of characteristics,
Leray's Theory of hyperbolic systems and techniques
developed by Choquet-Bruhat for ordinary spatial Cauchy
problems related to (YMV) systems.
Submitted July 16, 2010. Published December 13, 2011.
Math Subject Classifications: 81Q13, 35L45,35L55.
Key Words: Goursat problem; characteristic initial hypersurfaces;
Yang-Mills-Vlasov system; temporal gauge; initial
constraints; evolution problem.
Show me the PDF file (358 KB),
TEX file for this article.
 |
Marcel Dossa
Université de Yaoundé I, Faculté des Sciences
B.P. 812, Yaoundé, Cameroun
email: marceldossa@yahoo.fr
|
|---|
 |
Marcel Nanga
Université de N'Djaména
Faculté des Sciences Exactes et Appliquées
B.P. 1027, N'Djaména, Tchad
email: marnanga@yahoo.fr
|
|---|
Return to the EJDE web page
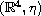 .
Under a
.
Under a
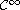 hypothesis on the data,
we solve the initial constraint problem and the evolution problem.
Local in time existence and uniqueness results are established
thanks to a suitable combination of the method of characteristics,
Leray's Theory of hyperbolic systems and techniques
developed by Choquet-Bruhat for ordinary spatial Cauchy
problems related to (YMV) systems.
hypothesis on the data,
we solve the initial constraint problem and the evolution problem.
Local in time existence and uniqueness results are established
thanks to a suitable combination of the method of characteristics,
Leray's Theory of hyperbolic systems and techniques
developed by Choquet-Bruhat for ordinary spatial Cauchy
problems related to (YMV) systems.

