We are concerned with the existence and uniqueness of solutions to nonlocal boundary-value problems on an interval
![$[a,c]$](gifs/aa.gif) for the
differential equation
for the
differential equation
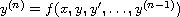 ,
where
,
where
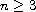 .
We use the method of matching solutions, with some
monotonicity conditions on
.
We use the method of matching solutions, with some
monotonicity conditions on
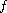 .
.
Xueyan Liu
Abstract:
We are concerned with the existence and uniqueness of solutions to
nonlocal boundary-value problems on an interval
![$[a,c]$](gifs/aa.gif) for the
differential equation
for the
differential equation
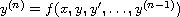 ,
where
,
where
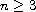 .
We use the method of matching solutions, with some
monotonicity conditions on
.
We use the method of matching solutions, with some
monotonicity conditions on
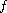 .
.
Submitted June 26, 2010. Published February 3, 2011.
Math Subject Classifications: 34B15, 34B10.
Key Words: Boundary value problem; nonlocal; matching solutions.
Show me the PDF file (219 KB), TEX file, and other files for this article.
 |
Xueyan (Sherry) Liu Department of Mathematics, Baylor University Waco, TX 76798-7328, USA email: Xueyan_Liu@baylor.edu |
|---|
Return to the EJDE web page