Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 24, pp. 1-12.
Continuous spectrum of a fourth order nonhomogeneous
elliptic equation with variable exponent
Abdesslem Ayoujil, Abdel Rachid El Amrouss
Abstract:
In this article, we consider the nonlinear eigenvalue problem
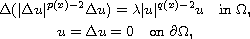
where
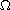 is a bounded domain in
is a bounded domain in
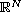 with smooth
boundary and
with smooth
boundary and
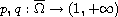 are
continuous functions. Considering different situations concerning
the growth rates involved in the above quoted problem, we prove the
existence of a continuous family of eigenvalues. The proofs of the
main results are based on the mountain pass lemma and Ekelandís
variational principle.
are
continuous functions. Considering different situations concerning
the growth rates involved in the above quoted problem, we prove the
existence of a continuous family of eigenvalues. The proofs of the
main results are based on the mountain pass lemma and Ekelandís
variational principle.
Submitted October 6, 2010. Published February 9, 2011.
Math Subject Classifications: 35G30, 35K61, 46E35.
Key Words: Fourth order elliptic equation; eigenvalue;
Navier condition; variable exponent; Sobolev space;
mountain pass theorem; Ekelandís variational principle.
Show me the PDF file (248 KB),
TEX file for this article.
 |
Abdesslem Ayoujil
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: abayoujil@yahoo.fr
|
|---|
 |
Abdel Rachid El Amrouss
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: elamrouss@fso.ump.ma
|
|---|
Return to the EJDE web page
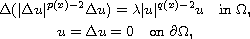
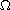 is a bounded domain in
is a bounded domain in
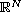 with smooth
boundary and
with smooth
boundary and
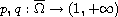 are
continuous functions. Considering different situations concerning
the growth rates involved in the above quoted problem, we prove the
existence of a continuous family of eigenvalues. The proofs of the
main results are based on the mountain pass lemma and Ekelandís
variational principle.
are
continuous functions. Considering different situations concerning
the growth rates involved in the above quoted problem, we prove the
existence of a continuous family of eigenvalues. The proofs of the
main results are based on the mountain pass lemma and Ekelandís
variational principle.

