We consider the nonlinear eigenvalue problem
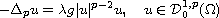
where
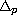 is the p-Laplacian operator,
is the p-Laplacian operator,
 is a connected domain in
is a connected domain in
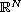 with
with
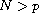 and the weight
function g is locally integrable. We obtain the existence
of a unique positive principal eigenvalue for g such
that
and the weight
function g is locally integrable. We obtain the existence
of a unique positive principal eigenvalue for g such
that
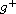 lies in certain subspace of weak-
lies in certain subspace of weak-
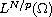 .
The radial symmetry of the first eigenfunctions are obtained for
radial g, when
.
The radial symmetry of the first eigenfunctions are obtained for
radial g, when
 is a ball centered at the origin or
is a ball centered at the origin or
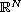 .
The existence of an infinite set of eigenvalues
is proved using the Ljusternik-Schnirelmann theory on
.
The existence of an infinite set of eigenvalues
is proved using the Ljusternik-Schnirelmann theory on
 manifolds.
manifolds.
