Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 70, pp. 1-14.
Structure of ground state solutions for singular elliptic
equations with a quadratic gradient term
Antonio Luiz Melo, Carlos Alberto Santos
Abstract:
We establish results on existence, non-existence, and
asymptotic behavior of ground state solutions for the
singular nonlinear elliptic problem

where
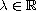 is a parameter,
is a parameter,
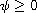 ,
not identically zero, is a locally Holder continuous function;
,
not identically zero, is a locally Holder continuous function;
 and
and
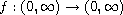 are continuous functions,
(possibly) singular in
are continuous functions,
(possibly) singular in
 ; that is,
; that is,
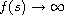 and either
and either
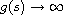 or
or
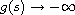 as
as
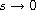 .
The main purpose of this article is to complement the main
theorem in Porru and Vitolo [15], for the case
.
The main purpose of this article is to complement the main
theorem in Porru and Vitolo [15], for the case
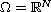 .
No monotonicity condition is imposed on f or g.
.
No monotonicity condition is imposed on f or g.
Submitted April 26, 2010. Published May 31, 2011.
Math Subject Classifications: 35J25, 35J20, 35J67.
Key Words: Singular elliptic equations; gradient term;
ground state solution.
Show me the PDF file (280 KB),
TEX file for this article.
 |
Antônio Luiz Melo
Department of Mathematics, University of Brasília
Planaltina, 70910-990, Brazil
email: almelo@unb.br
|
|---|
 |
Carlos Alberto Santos
Department of Mathematics, University of Brasília
Brasília, 70910-900, Brazil
email: csantos@unb.br, capdsantos@gmail.com
|
|---|
Return to the EJDE web page

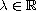 is a parameter,
is a parameter,
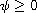 ,
not identically zero, is a locally Holder continuous function;
,
not identically zero, is a locally Holder continuous function;
 and
and
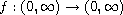 are continuous functions,
(possibly) singular in
are continuous functions,
(possibly) singular in
 ; that is,
; that is,
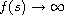 and either
and either
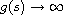 or
or
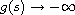 as
as
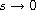 .
The main purpose of this article is to complement the main
theorem in Porru and Vitolo [15], for the case
.
The main purpose of this article is to complement the main
theorem in Porru and Vitolo [15], for the case
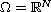 .
No monotonicity condition is imposed on f or g.
.
No monotonicity condition is imposed on f or g.

