Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 76, pp. 1-25.
A linear first-order hyperbolic equation
with discontinuous coefficient: distributional shadows
and propagation of singularities
Hideo Deguchi
Abstract:
It is well-known that distributional solutions to the Cauchy
problem for
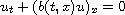 with
with
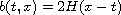 ,
where H is the Heaviside function, are non-unique.
However, it has a unique generalized solution in the sense
of Colombeau. The relationship between its generalized solutions
and distributional solutions is established.
Moreover, the propagation of singularities is studied.
,
where H is the Heaviside function, are non-unique.
However, it has a unique generalized solution in the sense
of Colombeau. The relationship between its generalized solutions
and distributional solutions is established.
Moreover, the propagation of singularities is studied.
Submitted January 19, 2011. Published June 16, 2011.
Math Subject Classifications: 46F30, 35L03, 35A21.
Key Words: First-order hyperbolic equation;
discontinuous coefficient; generalized solutions.
Show me the PDF file (351 KB),
TEX file for this article.
Hideo Deguchi
Department of Mathematics, University of Toyama
Toyama 930-8555, Japan
email: hdegu@sci.u-toyama.ac.jp
|
Return to the EJDE web page
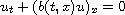 with
with
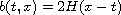 ,
where H is the Heaviside function, are non-unique.
However, it has a unique generalized solution in the sense
of Colombeau. The relationship between its generalized solutions
and distributional solutions is established.
Moreover, the propagation of singularities is studied.
,
where H is the Heaviside function, are non-unique.
However, it has a unique generalized solution in the sense
of Colombeau. The relationship between its generalized solutions
and distributional solutions is established.
Moreover, the propagation of singularities is studied.