Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 80, pp. 1-5.
Hyers-Ulam stability for second-order linear differential
equations with boundary conditions
Pasc Gavruta, Soon-Mo Jung, Yongjin Li
Abstract:
We prove the Hyers-Ulam stability of linear differential
equations of second-order with boundary conditions or
with initial conditions. That is, if y is an approximate
solution of the differential equation
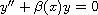 with
with
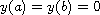 , then there exists an exact solution
of the differential equation, near y.
, then there exists an exact solution
of the differential equation, near y.
Submitted April 26, 2011. Published June 20, 2011.
Math Subject Classifications: 34K20, 26D10.
Key Words: Hyers-Ulam stability, differential equation.
Show me the PDF file (164 KB),
TEX file for this article.
 |
Pasc Gavruta
Department of Mathematics, University Politehnica of Timisoara
Piata Victoriei, No. 2, 300006 Timisoara, Romania
email: pgavruta@yahoo.com
|
|---|
 |
Soon-Mo Jung
Mathematics Section, College of Science and Technology
Hongik University, 339-701 Jochiwon, Korea
email: smjung@hongik.ac.kr
|
|---|
 |
Yongjin Li
Department of Mathematics, Sun Yat-Sen University
Guangzhou 510275, China
email: stslyj@mail.sysu.edu.cn
|
|---|
Return to the EJDE web page
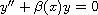 with
with
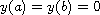 , then there exists an exact solution
of the differential equation, near y.
, then there exists an exact solution
of the differential equation, near y.


