This article presents the homogenization of a quasilinear elliptic-parabolic problem in an
 -periodic medium
consisting of a set of highly anisotropic fibers surrounded by
coating layers, the whole being embedded in a third material
having an order 1 conductivity. The conductivity along the
fibers is of order 1 but the conductivities in the transverse
directions and in the coatings are scaled by
-periodic medium
consisting of a set of highly anisotropic fibers surrounded by
coating layers, the whole being embedded in a third material
having an order 1 conductivity. The conductivity along the
fibers is of order 1 but the conductivities in the transverse
directions and in the coatings are scaled by
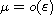 and
and
 ,
as
,
as
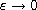 ,
respectively. The heat
flux are quasilinear, monotone functions of the temperature
gradient. The heat capacities of the medium components are bounded
but may vanish on certain subdomains, so the problem may become
degenerate. By using the two-scale convergence method, we can
derive the two-scale homogenized systems and prove some
corrector-type results depending on the critical value
,
respectively. The heat
flux are quasilinear, monotone functions of the temperature
gradient. The heat capacities of the medium components are bounded
but may vanish on certain subdomains, so the problem may become
degenerate. By using the two-scale convergence method, we can
derive the two-scale homogenized systems and prove some
corrector-type results depending on the critical value
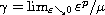 .
.
