Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 08, pp. 1-6.
Simplicity and stability of the first eigenvalue
of a (p;q) Laplacian system
Ghasem A. Afrouzi, Maryam Mirzapour, Qihu Zhang
Abstract:
This article concerns special properties of the principal
eigenvalue of a nonlinear elliptic system with
Dirichlet boundary conditions. In particular, we show
the simplicity of the first eigenvalue of
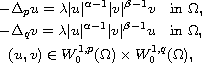
with respect to the exponents p and q, where
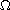 is
a bounded domain in
is
a bounded domain in
 .
.
Submitted November 3, 2011. Published January 12, 2012.
Math Subject Classifications: 35J60, 35B30, 35B40.
Key Words: Eigenvalue problem; quasilinear operator;
simplicity; stability.
An addendum was posted on July 21, 2016.
It states that some parts were copied from reference [6] without mentioning the
source. See the last page of this article.
Show me the PDF file (195 KB),
TEX file for this article.
 |
Ghasem Alizadeh Afrouzi
Department of Mathematics,
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Maryam Mirzapour
Department of Mathematics,
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email mirzapour@stu.umz.ac.ir
|
|---|
| |
Qihu Zhang
Department of Mathematics and Information Science
Zhengzhou University of Light Industry
Zhengzhou, Henan 450002, China
email: zhangqh1999@yahoo.com.cn
|
|---|
Return to the EJDE web page
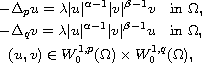
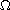 is
a bounded domain in
is
a bounded domain in
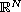 .
.

