Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 120, pp. 1-14.
Solutions of p(x)-Laplacian equations with critical exponent and
perturbations in R^N
Xia Zhang, Yongqiang Fu
Abstract:
Based on the theory of variable exponent Sobolev spaces,
we study a class of
 -Laplacian equations in
-Laplacian equations in
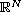 involving the critical exponent.
Firstly, we modify the principle of concentration compactness in
involving the critical exponent.
Firstly, we modify the principle of concentration compactness in
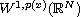 and obtain a new type of Sobolev inequalities
involving the atoms. Then, by using variational method, we obtain the
existence of weak solutions when the perturbation is small enough.
and obtain a new type of Sobolev inequalities
involving the atoms. Then, by using variational method, we obtain the
existence of weak solutions when the perturbation is small enough.
Submitted June 19, 2012. Published July 19, 2012.
Math Subject Classifications: 35J60, 46E35.
Key Words: Variable exponent Sobolev space; critical exponent; weak solution.
Show me the PDF file (261 KB),
TEX file for this article.
 |
Xia Zhang
Department of Mathematics, Harbin Institute of Technology
Harbin 150001, China.
Department of Mathematics, Pohang University of Science and
Technology
Pohang, Korea
email: piecesummer1984@163.com
|
|---|
 |
Yongqiang Fu
Department of Mathematics, Harbin Institute of Technology
Harbin 150001, China.
email: fuyqhagd@yahoo.cn
|
|---|
Return to the EJDE web page
 -Laplacian equations in
-Laplacian equations in
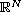 involving the critical exponent.
Firstly, we modify the principle of concentration compactness in
involving the critical exponent.
Firstly, we modify the principle of concentration compactness in
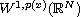 and obtain a new type of Sobolev inequalities
involving the atoms. Then, by using variational method, we obtain the
existence of weak solutions when the perturbation is small enough.
and obtain a new type of Sobolev inequalities
involving the atoms. Then, by using variational method, we obtain the
existence of weak solutions when the perturbation is small enough.

