Electron. J. Diff. Equ., Vol. 2012 (2012), No. 141, pp. 1-12.

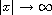
Behavior of the maximal solution of the Cauchy problem for some nonlinear pseudoparabolic equation as $|x|\to\infty$

Tatiana Kavitova

Abstract:
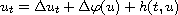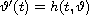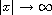We prove a comparison principle for solutions of the Cauchy problem of the nonlinear pseudoparabolic equation $u_t=\Delta u_t+ \Delta\varphi(u) +h(t,u)$ with nonnegative bounded initial data. We show stabilization of a maximal solution to a maximal solution of the Cauchy problem for the corresponding ordinary differential equation $\vartheta'(t)=h(t,\vartheta)$ as $|x|\to\infty$ under certain conditions on an initial datum.

Submitted March 22, 2012. Published August 20, 2012.
Math Subject Classifications: 35B40, 35B51, 35K70.
Key Words: Pseudoparabolic equation; comparison principle; stabilization.

Show me the PDF file (272 KB), TEX file, and other files for this article.

Tatiana Kavitova
Department of Mathematics, Vitebsk State University
Moskovskii pr. 33, 210038 Vitebsk, Belarus
email: KavitovaTV@tut.by

Return to the EJDE web page