Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 16, pp. 1-15.
Multiple solutions for a q-Laplacian equation on an annulus
Shijian Tai, Jiangtao Wang
Abstract:
In this article, we study the q-Laplacian equation
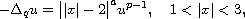
where
 and
and
 .
We prove that the problem has two solutions when
.
We prove that the problem has two solutions when
 is large, and has two additional solutions when
is large, and has two additional solutions when
 is close to
the critical Sobolev exponent
is close to
the critical Sobolev exponent
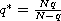 .
A symmetry-breaking phenomenon appears which shows that the
least-energy solution cannot be radial function.
.
A symmetry-breaking phenomenon appears which shows that the
least-energy solution cannot be radial function.
Submitted November 7, 2011. Published January 24, 2012.
Math Subject Classifications: 35J40.
Key Words: Ground state; minimizer; nonradial function;
q-Laplacian; Rayleigh quotient.
Show me the PDF file (277 KB),
TEX file for this article.
 |
Shijian Tai
Shenzhen Experimental Education Group
Shenzhen, 5182028, China
email: 363846618@qq.com
|
|---|
 |
Jiangtao Wang
School of Statistics and Mathematics
Zhongnan University of Economics and Law
Wuhan, 430073, China
email: wjtao1983@yahoo.com.cn
|
|---|
Return to the EJDE web page
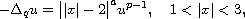
 and
and
 .
We prove that the problem has two solutions when
.
We prove that the problem has two solutions when
 is large, and has two additional solutions when
is large, and has two additional solutions when
 is close to
the critical Sobolev exponent
is close to
the critical Sobolev exponent
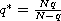 .
A symmetry-breaking phenomenon appears which shows that the
least-energy solution cannot be radial function.
.
A symmetry-breaking phenomenon appears which shows that the
least-energy solution cannot be radial function.

