Local and nonlocal reaction-diffusion models have been shown to demonstrate nontrivial steady state patterns known as Turing patterns. That is, solutions which are initially nearly homogeneous form non-homogeneous patterns. This paper examines the pattern selection mechanism in systems which contain nonlocal terms. In particular, we analyze a mixed reaction-diffusion system with Turing instabilities on rectangular domains with periodic boundary conditions. This mixed system contains a homotopy parameter
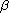 to vary the effect of both local
to vary the effect of both local
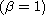 and nonlocal
and nonlocal
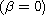 diffusion. The diffusion interaction length relative to the
size of the domain is given by a parameter
diffusion. The diffusion interaction length relative to the
size of the domain is given by a parameter
 .
We associate
the nonlocal diffusion with a convolution kernel, such that the
kernel is of order
.
We associate
the nonlocal diffusion with a convolution kernel, such that the
kernel is of order
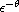 in the limit as
in the limit as
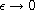 .
We prove that as long as
.
We prove that as long as
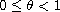 ,
in the singular limit as
,
in the singular limit as
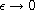 ,
the selection of patterns is determined by the
linearized equation. In contrast, if
,
the selection of patterns is determined by the
linearized equation. In contrast, if
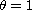 and
and
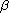 is small, our numerics show that pattern selection is a fundamentally
nonlinear process.
is small, our numerics show that pattern selection is a fundamentally
nonlinear process.

