Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 178, pp. 1-12.
Subharmonic solutions for nonautonomous
second-order Hamiltonian systems
Mohsen Timoumi
Abstract:
In this article, we prove the existence of subharmonic solutions for
the non-autonomous second-order Hamiltonian system
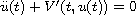 .
Also we study the minimality of their periods, when the nonlinearity
.
Also we study the minimality of their periods, when the nonlinearity
 grows faster than
grows faster than
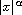 ,
,
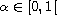 at infinity. The proof is based on the Least Action Principle
and the Saddle Point Theorem.
at infinity. The proof is based on the Least Action Principle
and the Saddle Point Theorem.
Submitted March 9, 2012. Published October 12, 2012.
Math Subject Classifications: 34C25.
Key Words: Hamiltonian systems; subharmonics; minimal periods;
saddle point theorem.
Show me the PDF file (242 KB),
TEX file for this article.
Mohsen Timoumi
Department of Mathematics,
Faculty of Sciences
5000 Monastir, Tunisia
email: m_timoumi@yahoo.com
|
Return to the EJDE web page
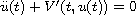 .
Also we study the minimality of their periods, when the nonlinearity
.
Also we study the minimality of their periods, when the nonlinearity
 grows faster than
grows faster than
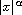 ,
,
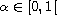 at infinity. The proof is based on the Least Action Principle
and the Saddle Point Theorem.
at infinity. The proof is based on the Least Action Principle
and the Saddle Point Theorem.