Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 182, pp. 1-16.
Weak-strong uniqueness of hydrodynamic flow of
nematic liquid crystals
Ji-hong Zhao, Qiao Liu
Abstract:
This article concerns a simplified model for a hydrodynamic system
of incompressible nematic liquid crystal materials. It is shown that
the weak-strong uniqueness holds for the class of weak solutions
provided that either
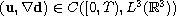 ;
or
;
or
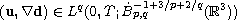 with
with
 ,
,
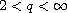 and
and
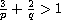 .
.
Submitted July 12, 2012. Published October 19, 2012.
Math Subject Classifications: 35A02, 35B35, 76A15.
Key Words: Nematic liquid crystal flow; weak solutions;
stability; weak-strong uniqueness.
Show me the PDF file (297 KB),
TEX file for this article.
 |
Ji-hong Zhao
College of Science, Northwest A&F University
Yangling, Shaanxi 712100, China
email: zhaojihong2007@yahoo.com.cn
|
|---|
 |
Qiao Liu
Department of Mathematics, Hunan Normal University
Changsha, Hunan 410081, China
email: liuqao2005@163.com
|
|---|
Return to the EJDE web page
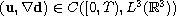 ;
or
;
or
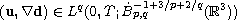 with
with
 ,
,
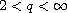 and
and
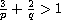 .
.

