Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 219, pp. 1-9.
Monotone iterative method for obtaining positive solutions
of integral boundary-value problems with phi-Laplacian operator
Yonghong Ding
Abstract:
This article concerns the existence, multiplicity of positive solutions
for the integral boundary-value problem with
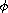 -Laplacian,
-Laplacian,
![$$\displaylines{
\big(\phi(u'(t))\big)'+f(t,u(t),u'(t))=0,\quad t\in[0,1],\cr
u(0)=\int_0^1 u(r)g(r)\,dr,\quad u(1)=\int_0^1u(r)h(r)\,dr,
}$$](gifs/ab.gif)
where
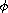 is an odd, increasing homeomorphism from R to R.
Using a monotone iterative technique,
we obtain the existence of positive solutions for this problem,
and present iterative schemes for approximating the solutions.
is an odd, increasing homeomorphism from R to R.
Using a monotone iterative technique,
we obtain the existence of positive solutions for this problem,
and present iterative schemes for approximating the solutions.
Submitted October 11, 2012. Published November 29, 2012.
Math Subject Classifications: 34B15, 34B18.
Key Words: phi-Laplacian; monotone iterative; cone; positive solutions.
Show me the PDF file (207 KB),
TEX file, and other files for this article.
 |
Yonghong Ding
Department of Mathematics
Tianshui Normal University
Tianshui 741000, China
email: dyh198510@126.com
|
|---|
Return to the EJDE web page
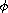 -Laplacian,
-Laplacian,
![$$\displaylines{
\big(\phi(u'(t))\big)'+f(t,u(t),u'(t))=0,\quad t\in[0,1],\cr
u(0)=\int_0^1 u(r)g(r)\,dr,\quad u(1)=\int_0^1u(r)h(r)\,dr,
}$$](gifs/ab.gif)
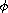 is an odd, increasing homeomorphism from R to R.
Using a monotone iterative technique,
we obtain the existence of positive solutions for this problem,
and present iterative schemes for approximating the solutions.
is an odd, increasing homeomorphism from R to R.
Using a monotone iterative technique,
we obtain the existence of positive solutions for this problem,
and present iterative schemes for approximating the solutions.
