Electron. J. Diff. Equ., Vol. 2012 (2012), No. 224, pp. 1-9.

Infinitely many large energy solutions of superlinear Schrodinger-Maxwell equations

Lin Li, Shang-Jie Chen

Abstract:
In this article we study the existence of infinitely many large energy solutions for the superlinear Schrodinger-Maxwell equations
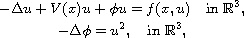
$$\displaylines{ -\Delta u+V(x)u+ \phi u=f(x,u) \quad \hbox{in }\mathbb{R}^3,\cr -\Delta \phi=u^2, \quad \hbox{in }\mathbb{R}^3, }$$
via the Fountain Theorem in critical point theory. In particular, we do not use the classical Ambrosetti-Rabinowitz condition.

Submitted July 10, 2012. Published December 11, 2012.
Math Subject Classifications: 35J35, 35J60, 47J30, 58E05.
Key Words: Schrodinger-Maxwell equations; superlinear; fountain theorem; variational methods.

Show me the PDF file (244 KB), TEX file, and other files for this article.

Lin Li
School of Mathematics and Statistics
Southwest University, Chongqing 400715, China
Department of Science, Sichuan University of Science and Engineering
Zigong 643000, China
email: lilin420@gmail.com
Shang-Jie Chen
School of Mathematics and Statistics
Chongqing Technology and Business University
Chongqing 400067, China
email: 11183356@qq.com

Return to the EJDE web page