Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 239, pp. 1-10.
Positive solutions for nonlinear elliptic systems
Adel Ben Dekhil
Abstract:
In this article, we study the existence of positive solutions for the system
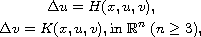
where
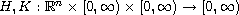 are continuous functions satisfying
are continuous functions satisfying
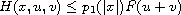 and
and
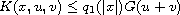 .
In terms of the growth of the variable potential functions
.
In terms of the growth of the variable potential functions
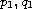 and the nonlinearities F and G, we establish some sufficient
conditions for the existence of positive continuous solutions for
this system and we discuss whether these solutions are bounded
or blow up at infinity.
and the nonlinearities F and G, we establish some sufficient
conditions for the existence of positive continuous solutions for
this system and we discuss whether these solutions are bounded
or blow up at infinity.
Submitted October 14, 2012. Published December 28, 2012.
Math Subject Classifications: 35B08, 35B09, 35J47.
Key Words: Semilinear elliptic systems; positive large solution;
positive bounded solution.
Show me the PDF file (230 KB),
TEX file for this article.
 |
Adel Ben Dekhil
Département de Mathématiques
Faculté des Sciences de Tunis
Université de Tunis El Manar
Campus Universitaire, 2092 Tunis, Tunisia
email: Adel.Bendekhil@ipein.rnu.tn
|
|---|
Return to the EJDE web page
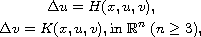
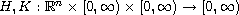 are continuous functions satisfying
are continuous functions satisfying
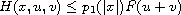 and
and
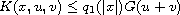 .
In terms of the growth of the variable potential functions
.
In terms of the growth of the variable potential functions
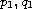 and the nonlinearities F and G, we establish some sufficient
conditions for the existence of positive continuous solutions for
this system and we discuss whether these solutions are bounded
or blow up at infinity.
and the nonlinearities F and G, we establish some sufficient
conditions for the existence of positive continuous solutions for
this system and we discuss whether these solutions are bounded
or blow up at infinity.
