Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 36, pp. 1-9.
Normal extensions of a singular multipoint differential
operator of first order
Zameddin I. Ismailov, Rukiye Ozturk Mert
Abstract:
In this work, we describe all normal extensions of the minimal
operator generated by linear singular multipoint formally normal differential
expression
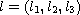 ,
,
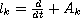 with selfadjoint operator
coefficients
with selfadjoint operator
coefficients
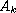 in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
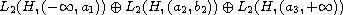
where
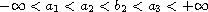 .
Also, we study the structure of the spectrum of these extensions.
.
Also, we study the structure of the spectrum of these extensions.
Submitted August 10, 2011. Published Match 7, 2012.
Math Subject Classifications: 47A10, 47A20.
Key Words: Multipoint differential operators; selfadjoint and normal extension;
spectrum.
Show me the PDF file (217 KB),
TEX file, and other files for this article.
 |
Zameddin I. Ismailov
Department of Mathematics, Faculty of Sciences
Karadeniz Technical University
61080, Trabzon, Turkey
email: zameddin@yahoo.com
|
|---|
 |
Rukiye Öztürk Mert
Department of Mathematics, Art and Science Faculty
Hitit University
19030, Corum, Turkey
email: rukiyeozturkmert@hitit.edu.tr
|
|---|
Return to the EJDE web page
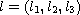 ,
,
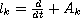 with selfadjoint operator
coefficients
with selfadjoint operator
coefficients
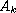 in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
in a Hilbert space.
This is done as a direct sum of Hilbert spaces of vector-functions
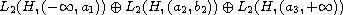
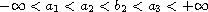 .
Also, we study the structure of the spectrum of these extensions.
.
Also, we study the structure of the spectrum of these extensions.

