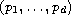 -Laplacian in
-Laplacian in
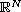
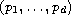 -Laplacian in
-Laplacian in
Dragos-Patru Covei
Abstract:
The main goal is to study nonlinear Schrodinger type
problems for the
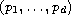 -Laplacian with
nonlinearities satisfying Keller- Osserman conditions.
We establish the existence of infinitely many positive entire radial
solutions by an application of a fixed point theorem and the
Arzela-Ascoli theorem. An important aspect in this article is that
the solutions are obtained by successive approximations and hence
the proof can be implemented in a computer program.
-Laplacian with
nonlinearities satisfying Keller- Osserman conditions.
We establish the existence of infinitely many positive entire radial
solutions by an application of a fixed point theorem and the
Arzela-Ascoli theorem. An important aspect in this article is that
the solutions are obtained by successive approximations and hence
the proof can be implemented in a computer program.
Submitted March 12, 2012. Published May 2, 2012.
Math Subject Classifications: 35J62, 35J66, 35J92, 58J10, 58J20.
Key Words: Entire solutions; large solutions; quasilinear systems;
radial solutions.
Show me the PDF file (237 KB), TEX file for this article.
 |
Dragos-Patru C. Covei Department of Development Constantin Brancusi University from Tg-Jiu Str. Grivitei, Nr. 1, Tg-Jiu, Romania email: coveipatru@yahoo.com |
|---|
Return to the EJDE web page