Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 68, pp. 1-11.
Limit cycles of the generalized Lienard differential equation
via averaging theory
Sabrina Badi, Amar Makhlouf
Abstract:
We apply the averaging theory of first and second order to a
generalized Lienard differential equation.
Our main result shows that for any
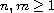 there are differential
equations
there are differential
equations
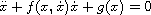 , with
f and g polynomials of degree n and m respectively,
having at most
, with
f and g polynomials of degree n and m respectively,
having at most
![$[n/2]$](gifs/ac.gif) and
and
![$\max\{[(n-1)/2]+[m/2], [n+(-1)^{n+1}/2]\}$](gifs/ad.gif) limit cycles, where
limit cycles, where
![$[\cdot]$](gifs/ae.gif) denotes the integer part function.
denotes the integer part function.
Submitted August 11, 2011. Published May 2, 2012.
Math Subject Classifications: 37G15, 37C80, 37C30.
Key Words: Limit cycle; averaging theory; Lienard differential equation
Show me the PDF file (226 KB),
TEX file for this article.
 |
Sabrina Badi
Department of Mathematics, University of Guelma
P.O. Box 401, Guelma 24000, Algeria
email: badisabrina@yahoo.fr
|
|---|
 |
Amar Makhlouf
Department of Mathematics, University of Annaba
P.O. Box 12, Annaba 23000, Algeria
email: makhloufamar@yahoo.fr
|
|---|
Return to the EJDE web page
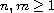 there are differential
equations
there are differential
equations
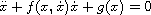 , with
f and g polynomials of degree n and m respectively,
having at most
, with
f and g polynomials of degree n and m respectively,
having at most
![$[n/2]$](gifs/ac.gif) and
and
![$\max\{[(n-1)/2]+[m/2], [n+(-1)^{n+1}/2]\}$](gifs/ad.gif) limit cycles, where
limit cycles, where
![$[\cdot]$](gifs/ae.gif) denotes the integer part function.
denotes the integer part function.

