We study the diffusion equation in the absence of instantaneous elasticity
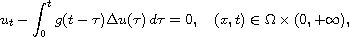
where
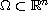 , subjected to nonlinear
boundary conditions. We prove that if the relaxation function
g decays exponentially, then the solutions is exponential stable.
, subjected to nonlinear
boundary conditions. We prove that if the relaxation function
g decays exponentially, then the solutions is exponential stable.
Mohammad Kafini
Abstract:
We study the diffusion equation in the absence of instantaneous elasticity
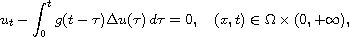
where
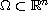 , subjected to nonlinear
boundary conditions. We prove that if the relaxation function
g decays exponentially, then the solutions is exponential stable.
, subjected to nonlinear
boundary conditions. We prove that if the relaxation function
g decays exponentially, then the solutions is exponential stable.
Submitted December 18, 2011. Published May 10, 2012.
Math Subject Classifications: 35B05, 35L05, 35L15, 35L70.
Key Words: Diffusion equation; instantaneous elasticity;
exponential decay; relaxation function; viscoelastic.
Show me the PDF file (219 KB), TEX file for this article.
 |
Mohammad Kafini Department of Mathematics and Statistics KFUPM, Dhahran 31261 Saudi Arabia email: mkafini@kfupm.edu.sa |
|---|
Return to the EJDE web page