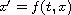 using inverse functions
using inverse functions
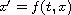 using inverse functions
using inverse functions
Jeffrey T. Hoag
Abstract:
A condition on the function f is given such that the scalar ordinary
differential equation
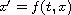 with initial condition
with initial condition
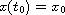 has a unique solution in a neighborhood of
has a unique solution in a neighborhood of
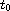 .
An example illustrates that this result can be used when other theorems
which put conditions on the difference
.
An example illustrates that this result can be used when other theorems
which put conditions on the difference
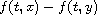 do not apply.
do not apply.
Submitted January 13, 2013. Published May 20, 2013.
Math Subject Classifications: 34A12.
Key Words: Existence; uniqueness; ordinary differential equation.
Show me the PDF file (152 KB), TEX file for this article.
 |
Jeffrey T. Hoag Mathematics Department Providence College Providence, RI 02918, USA email: jhoag@providence.edu |
|---|
Return to the EJDE web page