Using variational arguments, we study the existence and multiplicity of solutions for the degenerate nonlocal differential equation
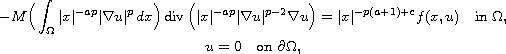
where
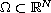 (
(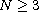 )
and the function
M may be zero at zero.
)
and the function
M may be zero at zero.
Nguyen Thanh Chung, Hoang Quoc Toan
Abstract:
Using variational arguments, we study the existence and multiplicity
of solutions for the degenerate nonlocal differential equation
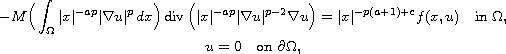
where
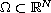 (
(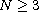 )
and the function
M may be zero at zero.
)
and the function
M may be zero at zero.
Submitted October 23, 2012. Published June 27, 2013.
Math Subject Classifications: 35J60, 35B38, 35J25.
Key Words: Degenerate nonlocal problems; existence o solutions;
multiplicity; variational methods.
A corrigendum was posted on August 21, 2014. It presents a proof of Lemma 2.4 with a modified assumption (F2), and without assumption (M2). This is necessary because there is no function satisying the original assumptions (M1) and (M2). See the last page of this article.
Show me the PDF file (267 KB), TEX file for this article.
 |
Nguyen Thanh Chung Dept. Science Management and International Cooperation Quang Binh University, 312 Ly Thuong Kiet Dong Hoi, Quang Binh, Vietnam email: ntchung82@yahoo.com |
|---|---|
 |
Hoang Quoc Toan Department of Mathematics, Hanoi University of Science 334 Nguyen Trai, Thanh Xuan, Hanoi, Vietnam email: hq_toan@yahoo.com |
Return to the EJDE web page