In this article, we investigate how the coefficient
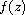 affects
the number of positive solutions of the quasilinear elliptic system
affects
the number of positive solutions of the quasilinear elliptic system
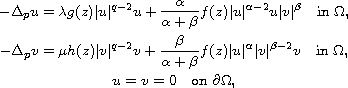
where
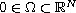 is a bounded domain,
is a bounded domain,
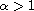 ,
,
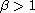 and
and
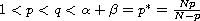 for
for
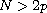 .
.
Qin Li, Zuodong Yang
Abstract:
In this article, we investigate how the coefficient
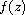 affects
the number of positive solutions of the quasilinear elliptic system
affects
the number of positive solutions of the quasilinear elliptic system
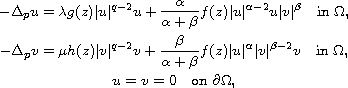
where
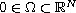 is a bounded domain,
is a bounded domain,
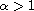 ,
,
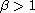 and
and
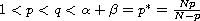 for
for
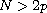 .
.
Submitted July 6, 2012. Published January 17, 2013.
Math Subject Classifications: 35J65, 35J50.
Key Words: Quasilinear elliptic systems; multiple positive solutions;
critical point, Nehari manifold.
Show me the PDF file (271 KB), TEX file for this article.
| Qin Li Institute of Mathematics, School of Mathematical Sciences Nanjing Normal University Jiangsu Nanjing, China email: 294973245@qq.com | |
 |
Zuodong Yang Institute of Mathematics, School of Mathematical Sciences Nanjing Normal University Jiangsu Nanjing, China email: zdyang_jin@263.net |
Return to the EJDE web page