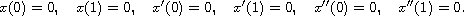Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 152, pp. 1-19.
Non-existence of solutions for two-point fractional and third-order
boundary-value problems
George L. Karakostas
Abstract:
In this article, we provide sufficient conditions for the
non-existence of solutions of the boundary-value problems with fractional
derivative of order
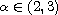 in the Riemann-Liouville sense
in the Riemann-Liouville sense
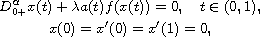
and in the Caputo sense

and for the third-order differential equation
![$$
x'''(t)+(Fx)(t)=0, \quad \hbox{a.e. }t\in [0,1],
$$](gifs/ad.gif)
associated with three among the following six conditions
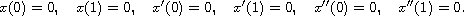
Thus, fourteen boundary-value problems at resonance and six
boundary-value problems at non-resonanse are studied.
Applications of the results are, also, given.
Submitted October 3, 2012. Published June 28, 2013.
Math Subject Classifications: 34B15, 34A10, 34B27, 34B99.
Key Words: Third order differential equation; two-point boundary-value problem;
fractional boundary condition; nonexistence of solutions.
Show me the PDF file (334 KB),
TEX file for this article.
 |
George L. Karakostas
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: gkarako@uoi.gr
|
|---|
Return to the EJDE web page
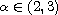 in the Riemann-Liouville sense
in the Riemann-Liouville sense
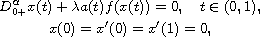

![$$
x'''(t)+(Fx)(t)=0, \quad \hbox{a.e. }t\in [0,1],
$$](gifs/ad.gif)