Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 154, pp. 1-16.
Global representations of the Heat and Schrodinger equation with
singular potential
Jose A. Franco, Mark R. Sepanski
Abstract:
The n-dimensional Schrodinger equation with a singular potential
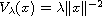 is studied.
Its solution space is studied as a global representation of
is studied.
Its solution space is studied as a global representation of
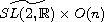 . A special subspace of solutions
for which the action globalizes is constructed via nonstandard
induction outside the semisimple category. The space of K-finite
vectors is calculated, obtaining conditions for
. A special subspace of solutions
for which the action globalizes is constructed via nonstandard
induction outside the semisimple category. The space of K-finite
vectors is calculated, obtaining conditions for
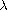 so that this
space is non-empty. The direct sum of solution spaces over such admissible
values of
so that this
space is non-empty. The direct sum of solution spaces over such admissible
values of
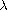 is studied as a representation of the (2n+1)-dimensional
Heisenberg group.
is studied as a representation of the (2n+1)-dimensional
Heisenberg group.
Submitted February 28, 2013. Published July 2, 2013.
Math Subject Classifications: 22E70, 35Q41.
Key Words: Schr\"{o}dinger equation; heat equation; singular potential;
Lie theory; \hfill\break\indent representation theory; globalization
Show me the PDF file (359 KB),
TEX file for this article.
 |
Jose A. Franco
University of North Florida
1 UNF Drive, Jacksonville, FL 32082, USA
email: jose.franco@unf.edu
|
|---|
 |
Mark R. Sepanski
Baylor University,
One Bear Place # 97328
Waco, TX 76798, USA
email: mark_sepanski@baylor.edu
|
|---|
Return to the EJDE web page
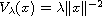 is studied.
Its solution space is studied as a global representation of
is studied.
Its solution space is studied as a global representation of
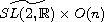 . A special subspace of solutions
for which the action globalizes is constructed via nonstandard
induction outside the semisimple category. The space of K-finite
vectors is calculated, obtaining conditions for
. A special subspace of solutions
for which the action globalizes is constructed via nonstandard
induction outside the semisimple category. The space of K-finite
vectors is calculated, obtaining conditions for
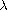 so that this
space is non-empty. The direct sum of solution spaces over such admissible
values of
so that this
space is non-empty. The direct sum of solution spaces over such admissible
values of
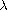 is studied as a representation of the (2n+1)-dimensional
Heisenberg group.
is studied as a representation of the (2n+1)-dimensional
Heisenberg group.

