Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 175, pp. 1-11.
Existence of positive bounded solutions
for nonlinear elliptic systems
Faten Toumi
Abstract:
In this article, we study a class of nonlinear elliptic systems
in regular domains of
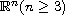 with compact boundary.
More precisely, we prove the existence of bounded positive continuous
solutions to the system
with compact boundary.
More precisely, we prove the existence of bounded positive continuous
solutions to the system
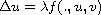 ,
,
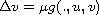 , subject to some Dirichlet conditions.
Our approach is essentially based on properties of functions in
a Kato class
, subject to some Dirichlet conditions.
Our approach is essentially based on properties of functions in
a Kato class
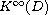 and the Schauder fixed point theorem.
and the Schauder fixed point theorem.
Submitted August 15, 2012. Published July 29, 2013.
Math Subject Classifications: 34B15, 34B27, 35J66.
Key Words: Green function; Kato class; nonlinear elliptic systems;
positive solution; Schauder fixed point theorem.
Show me the PDF file (244 KB),
TEX file, and other files for this article.
 |
Faten Toumi
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: faten.toumi@fsb.rnu.tn
|
|---|
Return to the EJDE web page
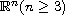 with compact boundary.
More precisely, we prove the existence of bounded positive continuous
solutions to the system
with compact boundary.
More precisely, we prove the existence of bounded positive continuous
solutions to the system
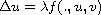 ,
,
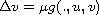 , subject to some Dirichlet conditions.
Our approach is essentially based on properties of functions in
a Kato class
, subject to some Dirichlet conditions.
Our approach is essentially based on properties of functions in
a Kato class
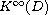 and the Schauder fixed point theorem.
and the Schauder fixed point theorem.
