Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 178, pp. 1-20.
Existence and blow-up of solutions for a semilinear filtration problem
Evangelos A. Latos, Dimitrios E. Tzanetis
Abstract:
We first examine the existence and uniqueness of local solutions
to the semilinear filtration equation
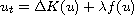 ,
for
,
for
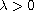 ,
with initial data
,
with initial data
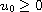 and appropriate boundary
conditions. Our main result is the proof of blow-up of solutions
for some
and appropriate boundary
conditions. Our main result is the proof of blow-up of solutions
for some
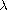 .
Moreover, we discuss the existence of solutions for the corresponding
steady-state problem. It is found that there exists a critical value
.
Moreover, we discuss the existence of solutions for the corresponding
steady-state problem. It is found that there exists a critical value
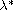 such that for
such that for
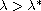 the problem has no
stationary solution of any kind, while for
the problem has no
stationary solution of any kind, while for
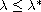 there exist classical stationary solutions.
Finally, our main result is that the solution for
there exist classical stationary solutions.
Finally, our main result is that the solution for
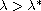 ,
blows-up in finite time independently of
,
blows-up in finite time independently of
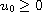 .
The functions f,K are positive, increasing and convex and K'/f
is integrable at infinity.
.
The functions f,K are positive, increasing and convex and K'/f
is integrable at infinity.
Submitted July 14, 2013. Published August 4, 2013.
Math Subject Classifications: 35K55, 35B44, 35B51, 76S05.
Key Words: Blow-up; filtration problem; existence; upper and lower solutions.
Show me the PDF file (460 KB),
TEX file for this article.
 |
Evangelos A. Latos
Institute for Mathematics and Scientific Computing
University of Graz
A-8010 Graz, Heinrichstrasse, 36, Austria
email: evangelos.latos@uni-graz.at
|
|---|
 |
Dimitrios E. Tzanetis
Department of Mathematics
School of Applied Mathematical and Physical Sciences
National Technical University of Athens, Zografou Campus
157 80 Athens, Greece
email: dtzan@math.ntua.gr
|
|---|
Return to the EJDE web page
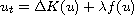 ,
for
,
for
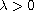 ,
with initial data
,
with initial data
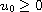 and appropriate boundary
conditions. Our main result is the proof of blow-up of solutions
for some
and appropriate boundary
conditions. Our main result is the proof of blow-up of solutions
for some
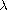 .
Moreover, we discuss the existence of solutions for the corresponding
steady-state problem. It is found that there exists a critical value
.
Moreover, we discuss the existence of solutions for the corresponding
steady-state problem. It is found that there exists a critical value
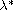 such that for
such that for
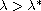 the problem has no
stationary solution of any kind, while for
the problem has no
stationary solution of any kind, while for
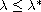 there exist classical stationary solutions.
Finally, our main result is that the solution for
there exist classical stationary solutions.
Finally, our main result is that the solution for
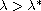 ,
blows-up in finite time independently of
,
blows-up in finite time independently of
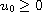 .
The functions f,K are positive, increasing and convex and K'/f
is integrable at infinity.
.
The functions f,K are positive, increasing and convex and K'/f
is integrable at infinity.

