Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 215, pp. 1-9.
Iterative technique for a third-order three-point BVP with
sign-changing Green's function
Jian-Ping Sun, Juan Zhao
Abstract:
In this article, by applying iterative technique,
we study the third-order three-point boundary value problem
![$$\displaylines{
u'''(t)=f(t,u(t)),\quad t\in [0,1], \cr
u'(0)=u''(\eta)=u(1)=0,
}$$](gifs/aa.gif)
where
![$f\in C([0,1]\times[0,+\infty),[0,+\infty))$](gifs/ab.gif) and
and
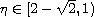 .
The emphasis is mainly that
although the corresponding Green's function is sign-changing, the
solution obtained is still positive. Moreover, our iterative scheme
starts off with zero function, which implies that the iterative
scheme is feasible. An example is also included to illustrate the
main results.
.
The emphasis is mainly that
although the corresponding Green's function is sign-changing, the
solution obtained is still positive. Moreover, our iterative scheme
starts off with zero function, which implies that the iterative
scheme is feasible. An example is also included to illustrate the
main results.
Submitted July 5, 2013. Published September 30, 2013.
Math Subject Classifications: 34B10, 34B18.
Key Words: Boundary value problem; Green's function; positive solution;
existence of solutions; iterative technique.
Show me the PDF file (188 KB),
TEX file for this article.
 |
Jian-Ping Sun
Department of Applied Mathematics
Lanzhou University of Technology,
Lanzhou, Gansu 730050, China
email: jpsun2012@163.com
|
|---|
 |
Juan Zhao
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu 730050, China
email: jzhao79@163.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
u'''(t)=f(t,u(t)),\quad t\in [0,1], \cr
u'(0)=u''(\eta)=u(1)=0,
}$$](gifs/aa.gif)
![$f\in C([0,1]\times[0,+\infty),[0,+\infty))$](gifs/ab.gif) and
and
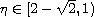 .
The emphasis is mainly that
although the corresponding Green's function is sign-changing, the
solution obtained is still positive. Moreover, our iterative scheme
starts off with zero function, which implies that the iterative
scheme is feasible. An example is also included to illustrate the
main results.
.
The emphasis is mainly that
although the corresponding Green's function is sign-changing, the
solution obtained is still positive. Moreover, our iterative scheme
starts off with zero function, which implies that the iterative
scheme is feasible. An example is also included to illustrate the
main results.

