Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 239, pp. 1-17.
Continuous dependence of solutions for indefinite semilinear
elliptic problems
Elves A. B. Silva, Maxwell L. Silva
Abstract:
We consider the superlinear elliptic problem
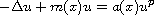
in a bounded smooth domain under Neumann boundary conditions,
where
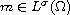 ,
,
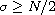 and
and
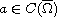 is a sign changing function.
Assuming that the associated first eigenvalue of the operator
is a sign changing function.
Assuming that the associated first eigenvalue of the operator
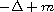 is zero, we use constrained minimization methods to
study the existence of a positive solution when
is zero, we use constrained minimization methods to
study the existence of a positive solution when
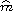 is a suitable perturbation of m.
is a suitable perturbation of m.
Submitted August 12, 2011. Published October 24, 2013.
Math Subject Classifications: 35J20, 35J60, 35Q55.
Key Words: Positive solution; constrained minimization; eigenvalue problem;
Neumann boundary condition; unique continuation.
Show me the PDF file (312 KB),
TEX file for this article.
 |
Elves A. B. Silva
Universidade de Brasília
Departamento de Matemática
Cep 70 910 900, Brasília-DF, Brazil
email: elves@unb.br
|
|---|
 |
Maxwell L. Silva
Universidade Federal de Goiás
Instituto de Matemática e Estatística
Cep 74 001 970, Goiania-GO, Brazil
email: maxwell@mat.ufg.br
|
|---|
Return to the EJDE web page
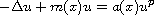
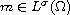 ,
,
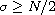 and
and
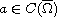 is a sign changing function.
Assuming that the associated first eigenvalue of the operator
is a sign changing function.
Assuming that the associated first eigenvalue of the operator
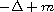 is zero, we use constrained minimization methods to
study the existence of a positive solution when
is zero, we use constrained minimization methods to
study the existence of a positive solution when
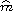 is a suitable perturbation of m.
is a suitable perturbation of m.

