Electron. J. Diff. Equ., Vol. 2013 (2013), No. 257, pp. 1-8.

Ground state solution of a nonlocal boundary-value problem

Cyril Joel Batkam

Abstract:
In this article, we apply the Nehari manifold method to study the Kirchhoff type equation
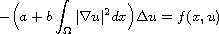
$$ -\Big(a+b\int_\Omega|\nabla u|^2dx\Big)\Delta u=f(x,u) $$
subject to Dirichlet boundary conditions. Under a general 4-superlinear condition on the nonlinearity f, we prove the existence of a ground state solution, that is a nontrivial solution which has least energy among the set of nontrivial solutions. If f is odd with respect to the second variable, we also obtain the existence of infinitely many solutions. Under our assumptions the Nehari manifold does not need to be of class C^1.

Submitted June 24, 2013. Published November 22, 2013.
Math Subject Classifications: 35J60, 35J25.
Key Words: Nonlocal problem; Kirchhoff's equation; ground state solution; Nehari manifold.

Show me the PDF file (214 KB), TEX file for this article.

Cyril Joel Batkam
Département de mathématiques
Université de Sherbrooke
Sherbrooke, Québec, J1K 2R1, Canada
email: cyril.joel.batkam@usherbrooke.ca

Return to the EJDE web page