Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 26, pp. 1-10.
A fixed point method for nonlinear equations involving a duality
mapping defined on product spaces
Jenica Cringanu, Daniel Pasca
Abstract:
The aim of this paper is to obtain solutions for the equation
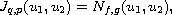
where
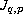 is the duality mapping on a product of two real,
reflexive and smooth Banach spaces
is the duality mapping on a product of two real,
reflexive and smooth Banach spaces
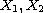 ,
corresponding to the
gauge functions
,
corresponding to the
gauge functions
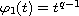 ,
,
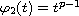 ,
,
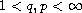 ,
,
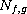 being the Nemytskii operator generated by
the Caratheodory functions f,g which satisfies some appropriate
conditions.
To prove the existence solutions we use a topological method via
Leray-Schauder degree.
As applications, we obtained in a unitary manner some existence results
for Dirichlet and Neumann problems for systems with (q,p)-Laplacian,
with (q,p)-pseudo-Laplacian or with
being the Nemytskii operator generated by
the Caratheodory functions f,g which satisfies some appropriate
conditions.
To prove the existence solutions we use a topological method via
Leray-Schauder degree.
As applications, we obtained in a unitary manner some existence results
for Dirichlet and Neumann problems for systems with (q,p)-Laplacian,
with (q,p)-pseudo-Laplacian or with
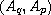 -Laplacian.
-Laplacian.
Submitted July 31, 2012. Published January 27, 2013.
Math Subject Classifications: 58C15, 35J20, 35J60, 35J65.
Key Words: Duality mapping; Leray-Schauder degree; (q,p)-Laplacian.
Show me the PDF file (222 KB),
TEX file for this article.
 |
Jenica Cringanu
Department of Mathematics, University of Galati
Str. Domneasca 47, Galati, Romania
email: jcringanu@ugal.ro
|
|---|
 |
Daniel Pasca
Department of Mathematics and Informatics,
University of Oradea
University Street 1, 410087 Oradea, Romania
email: dpasca@uoradea.ro
|
|---|
Return to the EJDE web page
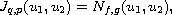
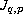 is the duality mapping on a product of two real,
reflexive and smooth Banach spaces
is the duality mapping on a product of two real,
reflexive and smooth Banach spaces
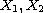 ,
corresponding to the
gauge functions
,
corresponding to the
gauge functions
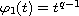 ,
,
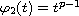 ,
,
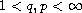 ,
,
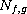 being the Nemytskii operator generated by
the Caratheodory functions f,g which satisfies some appropriate
conditions.
To prove the existence solutions we use a topological method via
Leray-Schauder degree.
As applications, we obtained in a unitary manner some existence results
for Dirichlet and Neumann problems for systems with (q,p)-Laplacian,
with (q,p)-pseudo-Laplacian or with
being the Nemytskii operator generated by
the Caratheodory functions f,g which satisfies some appropriate
conditions.
To prove the existence solutions we use a topological method via
Leray-Schauder degree.
As applications, we obtained in a unitary manner some existence results
for Dirichlet and Neumann problems for systems with (q,p)-Laplacian,
with (q,p)-pseudo-Laplacian or with
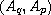 -Laplacian.
-Laplacian.

