Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 260, pp. 1-10.
Multiple solutions for perturbed non-local fractional Laplacian equations
Massimiliano Ferrara, Luca Guerrini, Binlin Zhang
Abstract:
In article we consider problems modeled by the non-local
fractional Laplacian equation
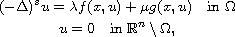
where
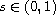 is fixed,
is fixed,
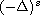 is the fractional
Laplace operator,
is the fractional
Laplace operator,
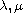 are real parameters,
are real parameters,
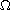 is an open bounded subset of
is an open bounded subset of
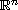 (
(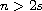 )
with Lipschitz boundary
)
with Lipschitz boundary
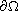 and
and
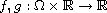 are two suitable Caratheodory functions.
By using variational methods in an appropriate abstract framework
developed by Servadei and Valdinoci [17] we prove
the existence of at least three weak solutions for certain values
of the parameters.
are two suitable Caratheodory functions.
By using variational methods in an appropriate abstract framework
developed by Servadei and Valdinoci [17] we prove
the existence of at least three weak solutions for certain values
of the parameters.
Submitted October 21, 2013. Published November 26, 2013.
Math Subject Classifications: 49J35, 35A15, 35S15, 47G20, 45G05.
Key Words: Variational methods; integrodifferential operators;
fractional Laplacian.
Show me the PDF file (244 KB),
TEX file for this article.
 |
Massimiliano Ferrara
University of Reggio Calabria and CRIOS University Bocconi of Milan
Via dei Bianchi presso Palazzo Zani
89127 Reggio Calabria, Italy
email: massimiliano.ferrara@unirc.it
|
|---|
 |
Luca Guerrini
Department of Management
University Polytecnic of Marche
Pizza Martelli 8, 60121 Ancona, Italy
email: luca.guerrini@univpm.it
|
|---|
 |
Binlin Zhang
MEDAlics Research Center, University Dante Alighieri
Via del Torrione, 89125 Reggio Calabria, Italy.
Department of Mathematics, Heilongjiang Institute of Technology
150050 Harbin, China
email: zhbinlin@gmail.com
|
|---|
Return to the EJDE web page
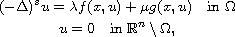
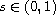 is fixed,
is fixed,
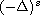 is the fractional
Laplace operator,
is the fractional
Laplace operator,
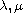 are real parameters,
are real parameters,
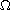 is an open bounded subset of
is an open bounded subset of
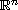 (
(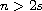 )
with Lipschitz boundary
)
with Lipschitz boundary
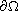 and
and
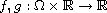 are two suitable Caratheodory functions.
By using variational methods in an appropriate abstract framework
developed by Servadei and Valdinoci [17] we prove
the existence of at least three weak solutions for certain values
of the parameters.
are two suitable Caratheodory functions.
By using variational methods in an appropriate abstract framework
developed by Servadei and Valdinoci [17] we prove
the existence of at least three weak solutions for certain values
of the parameters.


