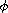 -Laplacian boundary-value
problems with integral boundary conditions
-Laplacian boundary-value
problems with integral boundary conditions
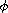 -Laplacian boundary-value
problems with integral boundary conditions
-Laplacian boundary-value
problems with integral boundary conditions
Wengui Yang
Abstract:
In this article, we study the existence, multiplicity,
and nonexistence of symmetric positive solutions for a class of
four-order integral boundary value problems with
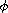 -Laplacian operator.
The arguments mainly rely on the Guo-Krasnosel'skii fixed point theorem
of cone expansion and compression of norm type and Leggett-Williams
fixed point theorem. Finally, some examples are presented to illustrate
the main results.
-Laplacian operator.
The arguments mainly rely on the Guo-Krasnosel'skii fixed point theorem
of cone expansion and compression of norm type and Leggett-Williams
fixed point theorem. Finally, some examples are presented to illustrate
the main results.
Submitted June 17, 2013. Published November 30, 2013.
Math Subject Classifications: 34B15, 34B18.
Key Words: Boundary value problems; integral boundary conditions;
symmetric positive solutions; \phi-Laplacian operator;
fixed point theorem.
Show me the PDF file (275 KB), TEX file for this article.
 |
Wengui Yang Ministry of Public Education Sanmenxia Polytechnic Sanmenxia 472000, China email: wgyang0617@yahoo.com |
|---|
Return to the EJDE web page