In this article, critical point theory is used to show the existence of nontrivial weak solutions to the quasilinear Schrodinger equation
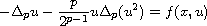
in a bounded smooth domain
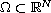 with Dirichlet
boundary conditions.
with Dirichlet
boundary conditions.
Duchao Liu
Abstract:
In this article, critical point theory is used to show the existence
of nontrivial weak solutions to the quasilinear Schrodinger equation
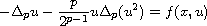
in a bounded smooth domain
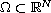 with Dirichlet
boundary conditions.
with Dirichlet
boundary conditions.
Submitted June 24, 2013. Published December 5, 2013.
Math Subject Classifications: 35B38, 35D05, 35J20.
Key Words: Quasilinear Schrodinger equation; soliton solution;
critical point theorem; fountain theorem; dual fountain theorem.
Show me the PDF file (259 KB), TEX file for this article.
 |
Duchao Liu School of Mathematics and Statistics Lanzhou University, Lanzhou 730000, China email: liuduchao@gmail.com Phone +8613893289235, fax +8609318912481 |
|---|
Return to the EJDE web page