Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 36, pp. 1-14.
Positive solutions for a 2nth-order p-Laplacian boundary
value problem involving all derivatives
Youzheng Ding, Jiafa Xu, Xiaoyan Zhang
Abstract:
In this work, we are mainly concerned with the positive
solutions for the 2nth-order p-Laplacian boundary-value
problem
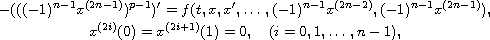
where
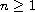 and
and
![$f\in C([0,1]\times \mathbb{R}_+^{2n},
\mathbb{R}_+)(\mathbb{R}_+:=[0,\infty))$](gifs/ac.gif) .
To overcome the difficulty resulting from all derivatives,
we first convert the above problem into a boundary value problem
for an associated second order integro-ordinary differential equation
with p-Laplacian operator. Then, by virtue of the classic fixed
point index theory, combined with a priori estimates of positive solutions,
we establish some results on the existence and multiplicity of positive
solutions for the above problem. Furthermore, our nonlinear term f is
allowed to grow superlinearly and sublinearly.
.
To overcome the difficulty resulting from all derivatives,
we first convert the above problem into a boundary value problem
for an associated second order integro-ordinary differential equation
with p-Laplacian operator. Then, by virtue of the classic fixed
point index theory, combined with a priori estimates of positive solutions,
we establish some results on the existence and multiplicity of positive
solutions for the above problem. Furthermore, our nonlinear term f is
allowed to grow superlinearly and sublinearly.
Submitted September 10, 2012. Published January 30, 2013.
Math Subject Classifications: 34B18, 45J05, 47H1.
Key Words: Integro-ordinary differential equation; a priori estimate;
index; fixed point; positive solution.
Show me the PDF file (253 KB),
TEX file, and other files for this article.
 |
Youzheng Ding
School of Mathematics, Shandong University
Jinan 250100, Shandong, China
email: dingyouzheng@139.com
|
|---|
 |
Jiafa Xu
School of Mathematics, Shandong University
Jinan 250100, Shandong, China
email: xujiafa292@sina.com
|
|---|
 |
Xiaoyan Zhang
School of Mathematics, Shandong University
Jinan 250100, Shandong, China
email: zxysd@sdu.edu.cn
|
|---|
Return to the EJDE web page
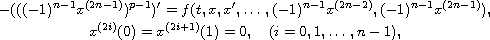
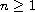 and
and
![$f\in C([0,1]\times \mathbb{R}_+^{2n},
\mathbb{R}_+)(\mathbb{R}_+:=[0,\infty))$](gifs/ac.gif) .
To overcome the difficulty resulting from all derivatives,
we first convert the above problem into a boundary value problem
for an associated second order integro-ordinary differential equation
with p-Laplacian operator. Then, by virtue of the classic fixed
point index theory, combined with a priori estimates of positive solutions,
we establish some results on the existence and multiplicity of positive
solutions for the above problem. Furthermore, our nonlinear term f is
allowed to grow superlinearly and sublinearly.
.
To overcome the difficulty resulting from all derivatives,
we first convert the above problem into a boundary value problem
for an associated second order integro-ordinary differential equation
with p-Laplacian operator. Then, by virtue of the classic fixed
point index theory, combined with a priori estimates of positive solutions,
we establish some results on the existence and multiplicity of positive
solutions for the above problem. Furthermore, our nonlinear term f is
allowed to grow superlinearly and sublinearly.


