Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 39, pp. 1-15.
Existence of traveling waves for diffusive-dispersive conservation laws
Cezar I. Kondo, Alex F. Rossini
Abstract:
In this work we show the existence existence and uniqueness of
traveling waves for diffusive-dispersive conservation laws with
flux function in
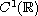 ,
by using phase plane analysis.
Also we estimate the domain of attraction of the equilibrium point
attractor corresponding to the right-hand state.
The equilibrium point corresponding to the left-hand state is a
saddle point. According to the phase portrait close to the saddle point,
there are exactly two semi-orbits of the system. We establish that
only one semi-orbit come in the domain of attraction
and converges to
,
by using phase plane analysis.
Also we estimate the domain of attraction of the equilibrium point
attractor corresponding to the right-hand state.
The equilibrium point corresponding to the left-hand state is a
saddle point. According to the phase portrait close to the saddle point,
there are exactly two semi-orbits of the system. We establish that
only one semi-orbit come in the domain of attraction
and converges to
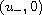 as
as
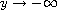 .
This provides the desired saddle-attractor connection.
.
This provides the desired saddle-attractor connection.
Submitted October 1, 2012. Published February 1, 2013.
Math Subject Classifications: 35L65, 76N10.
Key Words: Scalar conservation law; diffusive-dispersive; weak solution;
traveling wave; phase portrait.
Show me the PDF file (286 KB),
TEX file for this article.
 |
Cezar I. Kondo
Federal University of Sao Carlos
Department of Mathematics
P. O. Box 676 13565-905, Sao Carlos - SP, Brazil
email: dcik@dm.ufscar.br
|
|---|
 |
Alex F. Rossini
Federal University of Sao Carlos
Department of Mathematics
P. O. Box 676 13565-905, Sao Carlos - SP, Brazil
email: alexrossini@dm.ufscar.br
|
|---|
Return to the EJDE web page
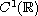 ,
by using phase plane analysis.
Also we estimate the domain of attraction of the equilibrium point
attractor corresponding to the right-hand state.
The equilibrium point corresponding to the left-hand state is a
saddle point. According to the phase portrait close to the saddle point,
there are exactly two semi-orbits of the system. We establish that
only one semi-orbit come in the domain of attraction
and converges to
,
by using phase plane analysis.
Also we estimate the domain of attraction of the equilibrium point
attractor corresponding to the right-hand state.
The equilibrium point corresponding to the left-hand state is a
saddle point. According to the phase portrait close to the saddle point,
there are exactly two semi-orbits of the system. We establish that
only one semi-orbit come in the domain of attraction
and converges to
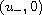 as
as
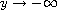 .
This provides the desired saddle-attractor connection.
.
This provides the desired saddle-attractor connection.

