In this article we study the existence of positive solutions for the nonlocal multi-point boundary-value problem

We also consider the corresponding integral condition, and the two special cases
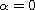 and
and
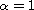 .
.
Ahmed M. A. El-Sayed, Ebtisam O. Bin-Taher
Abstract:
In this article we study the existence of positive solutions for
the nonlocal multi-point boundary-value problem

We also consider the corresponding integral condition, and the
two special cases
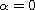 and
and
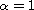 .
.
Submitted March 19, 2012. Published March 5, 2013.
Math Subject Classifications: 34B10, 26A33
Key Words: Fractional calculus; boundary value problem; nonlocal condition;
integral condition; positive solution.
An addendum was posted on December 4, 2013. It states that Theorem 3.2, the example, Corollary 3.3, and Corollary 3.4 are not correct. See the last page of this article.
Show me the PDF file (194 KB), TEX file for this article.
 |
Ahmed M. A. El-Sayed Faculty of Science, Alexandria University Alexandria, Egypt email: amasayed@hotmail.com |
|---|---|
| Ebtisam O. Bin-Taher Faculty of Science Hadhramout Univeristy of Science and Technology Hadhramout, Yemen email: ebtsamsam@yahoo.com |
Return to the EJDE web page