In this article, we consider the nonautonomous evolution problem
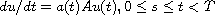 with initial condition
with initial condition
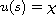 where -A generates a holomorphic semigroup of angle
where -A generates a holomorphic semigroup of angle
![$\theta \in (0,\pi/2]$](gifs/ac.gif) on a Banach space X and
on a Banach space X and
![$a\in C([0,T]:\mathbb{R}^+)$](gifs/ad.gif) .
The problem is generally ill-posed under such conditions, and so we employ
methods to approximate known solutions of the problem. In particular,
we prove the existence of a family of regularizing operators for the
problem which stems from the solution of an approximate well-posed problem.
In fact, depending on whether
.
The problem is generally ill-posed under such conditions, and so we employ
methods to approximate known solutions of the problem. In particular,
we prove the existence of a family of regularizing operators for the
problem which stems from the solution of an approximate well-posed problem.
In fact, depending on whether
![$\theta \in (0,\pi/2]$](gifs/ac.gif) or
or
![$\theta \in (\pi/4,\pi/2]$](gifs/ae.gif) ,
we provide two separate approximations each
yielding a regularizing family. The theory has applications to ill-posed
partial differential equations in
,
we provide two separate approximations each
yielding a regularizing family. The theory has applications to ill-posed
partial differential equations in
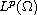 ,
,
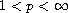 where A is a strongly elliptic differential operator and
where A is a strongly elliptic differential operator and
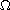 is a fixed
domain in
is a fixed
domain in
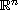 .
.
