In this article we study the Kirchhoff equation
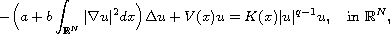
where
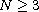 ,
,
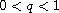 ,
,
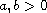 are constants and
are constants and
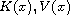 both
change sign in
both
change sign in
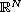 .
Under appropriate assumptions on
.
Under appropriate assumptions on
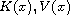 ,
the existence of infinitely many solutions is
proved by using the symmetric Mountain Pass Theorem.
,
the existence of infinitely many solutions is
proved by using the symmetric Mountain Pass Theorem.
Anouar Bahrouni
Abstract:
In this article we study the Kirchhoff equation
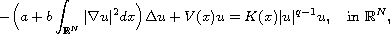
where
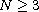 ,
,
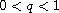 ,
,
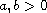 are constants and
are constants and
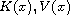 both
change sign in
both
change sign in
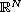 .
Under appropriate assumptions on
.
Under appropriate assumptions on
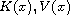 ,
the existence of infinitely many solutions is
proved by using the symmetric Mountain Pass Theorem.
,
the existence of infinitely many solutions is
proved by using the symmetric Mountain Pass Theorem.
Submitted March 6, 2013, Published April 16, 2013.
Math Subject Classifications: 35J60, 35J91, 58E30.
Key Words: Kirchhoff equations; symmetric Mountain Pass Theorem;
infinitely many solutions.
Show me the PDF file (227 KB), TEX file for this article.
 |
Anouar Bahrouni Mathematics Department, University of Monastir Faculty of Sciences, 5019 Monastir, Tunisia email: bahrounianouar@yahoo.fr, Fax + 216 73 500 278 |
|---|
Return to the EJDE web page